TUMGAD

Exercise generation and helpful materials for the Introduction to Algorithms and Data Structures 📚

AVL Trees

AVL Trees (names after Georgy Adelson-Velsky and Evgenii Landis) are balanced binary search trees. They solve the problem of binary search trees mutating into lists:

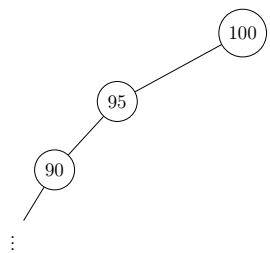
The mutation of a BST into a list

To achieve this, the trees manage so-called balances of their sub-trees which are calculated by subtracting the right sub-tree height from the left.

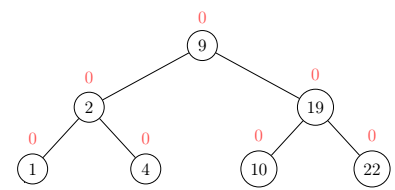
An example AVL Tree with every node’s balance in red:

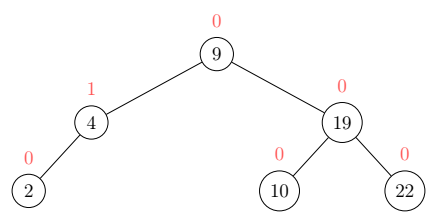
An AVL tree with the balance of every node noted in red

If the balance of any node reaches a threshold of 2, rebalancing in the form of rotation is in order. The kind of rotation needed is determined by the balances:

Parent balance	Child Balance	Rotation
2	1	right
-2	-1	left
2	-1	left-right
-2	1	right-left

Insert

Insertion into an AVL tree works just like in a BS Tree, just remember to keep track of the balances.

Example: Insert 1 into the above tree:

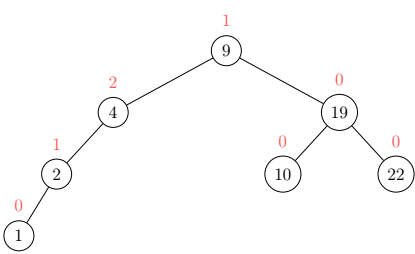
An unbalanced AVL tree with the balance of every node noted in red

As you can see the node with value 4 has a balance of 2 and its child node a balance of 1, thus a right-rotation is needed to satisfy the tree conditions:

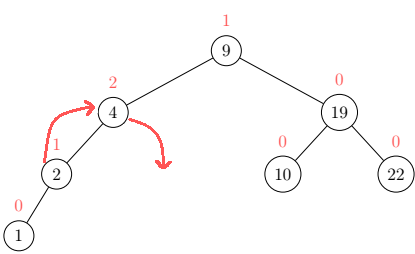
Beautiful rotation arrows brought to you by MS Paint

After Rotation the balances are

Deletion

Deleting a node from an AVL Tree is sometimes slightly more complicated. If the node is a leaf, you simply remove it, update balances and re-balance if necessary.

If the node is not a leaf, you switch it with its in-order predecessor (i.e. the maximum node in the left subtree), remove the node you want to remove (as it is now a leaf), update balances and re-balance if necessary.

Time Complexity:

Access	Search	Insertion	Deletion
`O(log n)`	`O(log n)`	`O(log n)`	`O(log n)`