TUMGAD
Exercise generation and helpful materials for the Introduction to Algorithms and Data Structures 📚
Binary Heaps
Binary Heaps are a kind of priority Queue, that always
take the shape of a binary tree. The tree
can be complete ((n+1)/2 leafs) or the last level of the
tree is incomplete, but the tree is filled from left
to right.
Example of a valid Binary Heap:
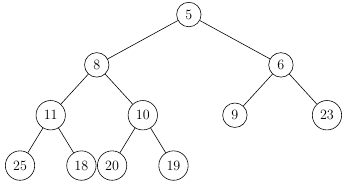
As you can see there is another special invariant present in the heap, the root of a (sub-)tree carries the minimal value in that tree. If this is the case the heap is called a min-heap (max-heap otherwise).
Insertion (example: 4)
When inserting a node into the heap, you have to first add it as a leaf at the first available position:
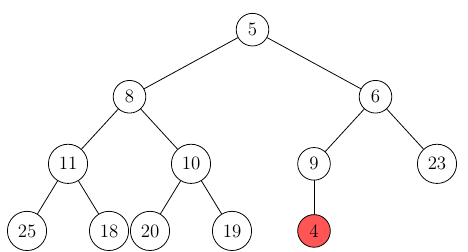
Afterwards, we need to make sure the invariant of the minimal value as the root is guaranteed, to do this, we compare the inserted node with its parent and swap the two if the parent is bigger (smaller in a max-heap).
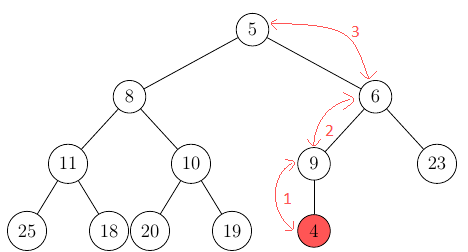
This operation of swapping the node until it is at its proper place is called siftUp() or (min/max)-heapify.
After we finished, the parent of the inserted node is either smaller, or the node is the root (the latter in this case).
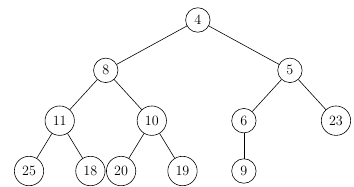
Removing the root
The point of priority Queues is that you always have a fairly simple and fast way to get to the element with the highest priority. In a Binary heap, this element is always the root node.
Removing the root is simple, you just swap it with the last leaf in the tree, delete it and then sift the new root down if the priority of one of the children is higher.
Example:
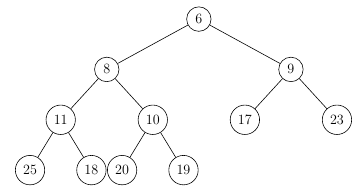
When removing the root out of this heap, you would
- Swap it with the last leaf (19)
- Delete 6 from its new leaf position
- Swap 19 with its minimal child until the invariant is re-established
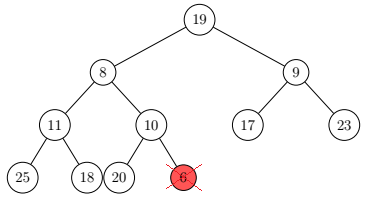
Step 1 and 2 (Swap and Deletion):
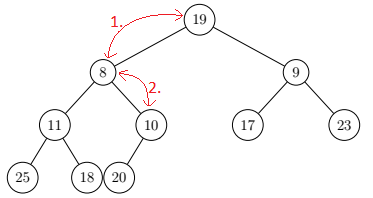
Step 3 (Sift):
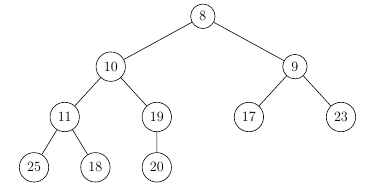
So after the entire deleteRoot() operation we’re left with a valid binary heap again:
HeapSort
Because of how these priority queues operate and their relative efficiency, they are quite useful for things like sorting algorithms.
As you might guess, if you insert n elements into the binary heap and then
remove the root n times, you can sort these elements based on their
priority. This algorithm is called heapsort.
As you can extract from the table below, the insertion into a tree
works in O(1) time, the deletion in O(log n). Thus
the insertion and subsequent deletion of n elements (HeapSort)
works in a worst-case time of O(n log n)
Time Complexity:
| Search | Insertion | Deletion |
|---|---|---|
O(n) |
O(1) |
O(log n) |