TUMGAD
Exercise generation and helpful materials for the Introduction to Algorithms and Data Structures 📚
Dijkstra’s Algorithm for Shortest Paths
Named after Edsger W. Dijkstra, the Dijkstra algorithm is a fairly simple approach to solving the problem of finding the shortest path between nodes in a weighted graph.
To achieve this the algorithm manages a special priority queue, in which the nodes and their respective distances are stored.
Consider the following example Graph:
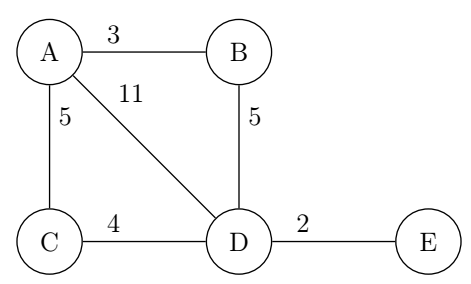
Say you want to find the shortest path to every node starting from A. This is what the algorithm would do step-by-step:
- Add A to the queue with a distance of 0
- Remove the first node from the queue
- Insert the neighbors of the removed node into the priority queue while adding up their distances with the distance of the first node
- Repeat 2 & 3 until you reached the desired node or every node has been visited
A lot of this iteration of the algorithm depends on the implementation of the priority queue, however:
insertIntoQueue(…):
- If the node is not already in the queue and never was in the queue (i.e. has not been visited) insert at priority and then lexicographically
- If the node is in the queue but with a lower priority (higher distance), update the distance and sort by priority and then lexicographically
So in the above example this is what the queue and its updates would look like:
| Priority Queue | Additions/Updates |
|---|---|
(B,3), (C,5) |
(B,3), (C,5) |
(C,5), (D,8) (E,10) |
(D,8), (E,10) |
(D,8) (E,10) |
- |
(E,10) |
- |
This tells us the shortest path to every node from node A:
(B,3),(C,5),(D,8),(E,10)
By working backwards with these shortest distances and the weights specified in the Graph, we get the shortest path from A to E:
A -> B -> D -> E