TUMGAD
Exercise generation and helpful materials for the Introduction to Algorithms and Data Structures 📚
Floyd-Warshall Algorithm (All Pairs Shortest Paths)
The Floyd-Warshall algorithm is one of the most simple algorithms that solves the problem of finding the shortest path between all pairs of nodes in a graph.
Trivially, in a graph with e.g. 5 nodes there are 20 distances to be considered (not counting the ones from a node to itself)
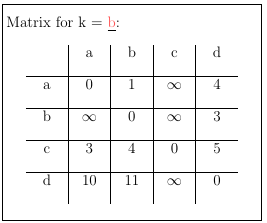
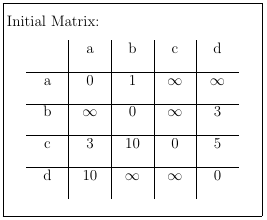
It is easiest to align this information in a table to keep track of the distances. Unknown/Unreachable distances are by definition filled with infinity.
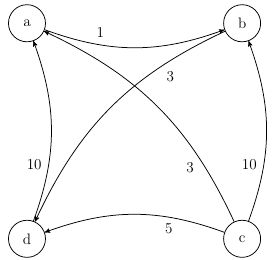
Consider the following example graph:
After initialization the table looks like this:
Now, step by step we look at the next node lexicographically (a first) and iterate through the column of a line by line. The node at the current step will be labelled x.
We will have to start another iteration over the line of a, call that y.
If the cell at [x][a] + [a][y] is smaller than [x][y], we update [x][y] to the value calculated.
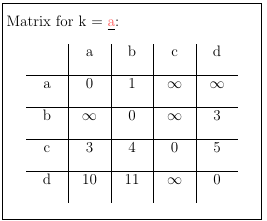
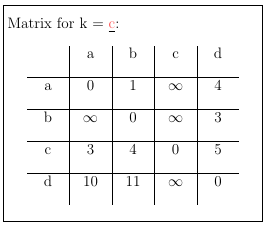
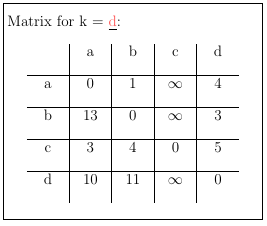
Repeat these steps for b, c and d to get the final matrix, with the shortest paths from one node to another.